PROBLEMAS DE GEOLOGÍA ESTRUCTURAL PARA LA GEOLOGÍA DEL BACHILLERATO: UN ACERCAMIENTO CUANTITATIVO A LOS MAPAS GEOLÓGICOS

PROBLEMAS DE GEOLOGÍA ESTRUCTURAL PARA LA GEOLOGÍA DEL BACHILLERATO: UN ACERCAMIENTO CUANTITATIVO A LOS MAPAS GEOLÓGICOSGeological Structures problems for Bachelors degree Geology: a quantitative approach to geological maps Jesús Duque

CONCEPTOS A TENER EN CUENTA PARA LOS PROBLEMAS DE LOS TRES PUNTOS

En este tipo de problemas se hacen equivalente los términos de capa o estrato con el de superficie geométrica plana, de momento las capas y estratos no tienen potencia es decir carecen de espesor.

Dirección de una capa: Es la dirección de la recta intersección de una capa con un plano horizontal imaginario. La dirección de una recta es el ángulo que forma con la dirección norte-sur. Se expresa mediante los grados de ese ángulo añadiendo el sentido respecto al cual se ha medido dicho ángulo. Así una dirección N35E, significa que la recta intersección forma 49 grados con la dirección norte-sur, medidos hacia el este. La misma dirección podría ser expresada N145W, el ángulo en este caso está medido en sentido oeste, comprueba que esos dos ángulos son suplementarios, y que sumados resultan 180º. Como es obvio una

capa horizontal no tiene dirección, ya que no produce una recta intersección con un plano igualmente horizontal; en este caso no se da la dirección de la capa, sino que simplemente se indica que dicha capa es horizontal.

Buzamiento de una capa: Es el ángulo de inclinación de una capa. Se expresa respecto a la horizontal, acompañado del sentido hacia el cual está inclinado; por ejemplo 76ºNW, esa capa está inclinada respecto a la horizontal 76º hacia el noroeste. Se simboliza con la letra griega ß. Tal vez se comprenda mejor con este sencillo bloque diagrama
Dirección de buzamiento real de una capa: Es la dirección de la perpendicular a la dirección de la capa, medida en un plano horizontal.

Buzamiento real de una capa ( ẞ ): Es el ángulo que forma la capa con el plano horizontal medido según el plano vertical que pasa por la dirección de buzamiento real.

Dirección de buzamiento aparente: Es cualquier dirección sobre el plano horizontal (exceptuando la dirección de buzamiento real y la dirección de la capa, en el primer caso la inclinación medida será la máxima y en el segundo no se medirá ninguna inclinación)

Buzamiento aparente (  ẞ´ ): Es el ángulo que forma la capa con el plano horizontal, medido según un plano vertical que pasa por una dirección de buzamiento aparente.

*Nota aclaratoria: El buzamiento real es el mayor que se puede medir sobre una capa determinada. Cuando se indique un buzamiento sin más, entenderemos que se trata del buzamiento real, ya que de referirse a un buzamiento aparente hay que indicarlo claramente. No olvidar añadir al ángulo de buzamiento el sentido de la medida o bien indicarlo gráficamente.

Horizontales de una capa: Son líneas intersección de la capa con planos horizontales a distintas cotas y que se proyecta sobre un plano de referencia a una cota determinada. Todas las horizontales de una capa son paralelas y cualquiera de ella define la dirección de la capa. Se identifican por la diferencia de cota respecto al plano de referencia. Ejemplo:

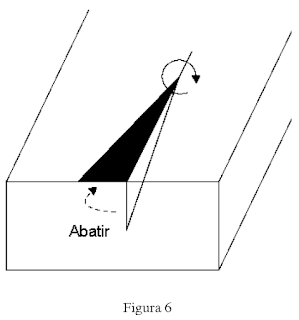
Abatir un plano: Es uno de los principales mecanismos para hacer posible la resolución gráficas de este tipo de problemas geológicos. Como nuestro papel es bidimensional y los datos y situación que plantean los problemas son tridimensionales, hay que abatir la tercera dimensión; así hay que proyectar los planos verticales de tal forma que conserven las medidas y proporciones (esto último es imprescindible ya que el resultado lo vamos a obtener mediante una medición en el gráfico).

El abatimiento de un plano consiste en transportarlo desde la vertical a la horizontal, girándolo sobre un eje que se debe encontrar en el plano sobre el que se realiza el abatimiento y que a su vez pertenece al plano abatido. Realizada esta sencilla operación, podemos medir en nuestro papel distancias y ángulos. Ejemplo:

PROBLEMAS DE LOS TRES PUNTOS
Son problemas en los que básicamente se trata de calcular la dirección y buzamientos tanto reales con aparentes de una capa o capas, conociendo los datos de tres puntos perteneciente a ella. Los problemas se pueden plantear de diferentes formas, de tal
manera que se puede conocer la dirección y buzamiento real pidiéndose buzamientos aparentes y cota de algunos puntos de la capa. Pero en definitiva el mecanismo de resolución es siempre el mismo.

Puede ocurrir:

• € Que los tres puntos se encuentren a la misma cota y que estén alineados. El problema está resulto, la dirección de la capa es la de la recta que pasa por esos tres puntos, para el buzamiento no hay datos.

• € Que dos puntos se encuentren a la misma cota y el tercero a diferente cota, pero no alineados. En este caso se deduce que la dirección de la recta que une los dos puntos de igual cota, es la dirección de la capa. Para hallar el buzamiento, se traza la perpendicular a la dirección de la capa (dirección de buzamiento real) que pase por el tercer punto, se marca la diferencia de cota, se abate el plano y el ángulo resultante es el buzamiento real de la capa.Todos los pasos se han de hacer a la misma escala.

• € Que los tres puntos estén a distinta cota, que como es lógico es la situación real más común. La situación se complica un poco. Hay que utilizar un aparato gráfico para obtener dos puntos a la misma cota y convertir el problema en uno del tipo anterior. Esto se explicará con un poco más de detenimiento en la introducción de subapartado correspondiente.

PILDORA EDUCATIVA ¿QUE SON LAS TECTONITAS?